Area tells you how much flat space a shape covers. Whether you’re tiling a floor, cutting fabric, designing a garden bed, or solving homework, the Area Calculator gives fast, accurate results for every common geometric shape. Pick a shape from the dropdown, enter the labeled dimensions, select units, and get the area instantly — plus helpful examples and measurement tips below.
Measurement and Field Tips
I’ve written math tools and guides for years, and these tips consistently save users from calculation blunders – gold mined from practical field experience!
- Always Consistent Units: Convert inches to cm or meters beforehand. Mixed units throw off the entire formula, frustration guaranteed.
- String Method for Tough Shapes: For large or irregular circles, wrap a flexible rope tightly around the circle, mark, then measure its length with a ruler – this is your spot-on circumference. It’s my signature trick in workshops!
- Diameter to Radius: Did you measure the diameter (from one end of the circle to the other)? If the tool asks for a radius, divide it by 2. Or enter the diameter directly if it accepts it – no hassle.
- Maintain Pi’s Precision: π≈3.14159 will do for everyday work; for engineering projects, turn on the calculator’s high-precision settings.
- Smart Rounding: Hold 4-6 significant figures in intermediate steps, and only round the final answer. Quick rounding reduces accuracy.
- Top Mistake to Avoid: Units mix-up, such as radius in cm and height in meters – the calculator will warn, but you’re on your way!
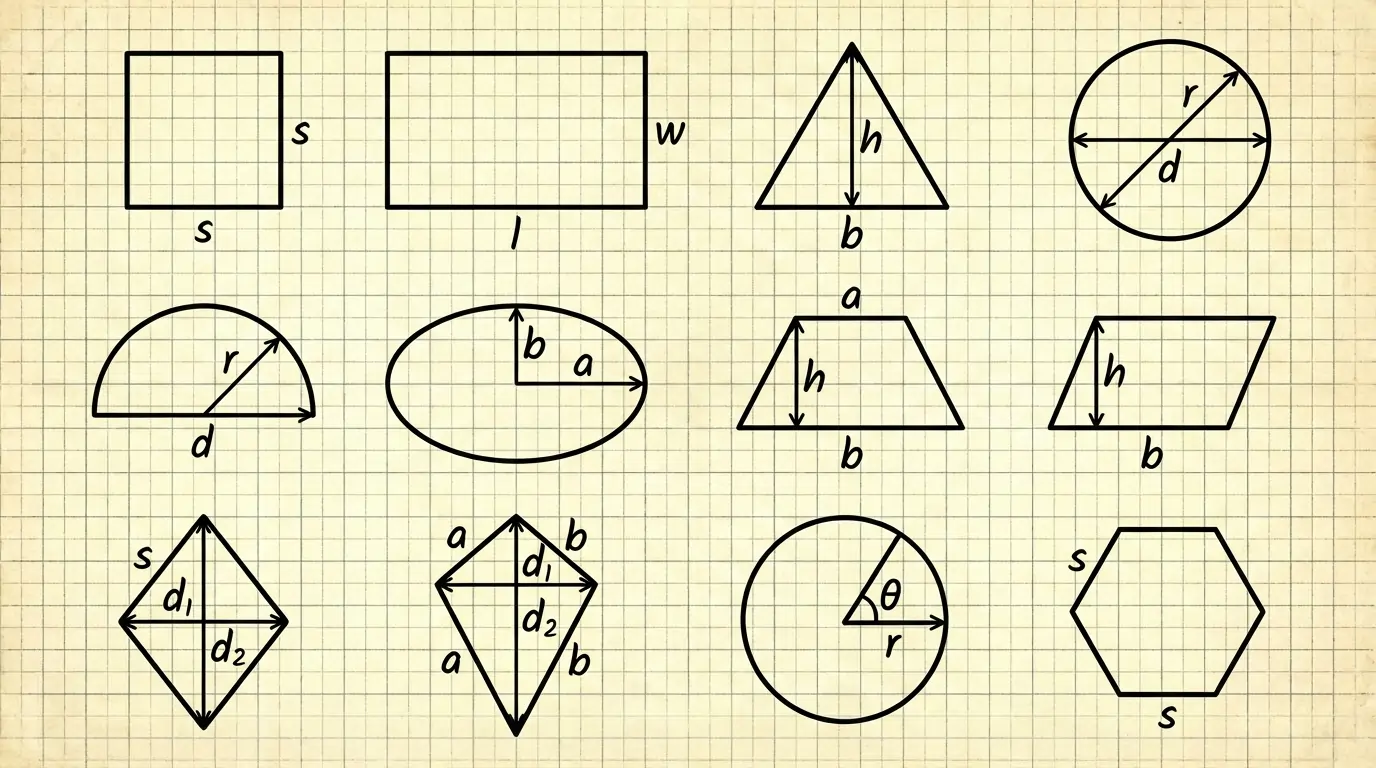
Area Formulas at a Glance
| Shape | Formula |
|---|---|
| Square | A = a2 |
| Rectangle | A = l × w |
| Triangle | A = (b × h) / 2 — or (Heron) A = ¼√{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)} |
| Circle | A = πr2 |
| Semicircle | A = (1/2)πr2 |
| Ellipse | A = πab (a, b are semi-axes) |
| Trapezoid | A = (a + b) × h / 2 |
| Parallelogram | A = base × height (or A = ab × sin(θ)) |
| Rhombus | A = (d1 × d2) / 2 |
| Kite | A = (d1 × d2) / 2 |
| Circle sector | A = (r2 × θ) / 2 (θ in radians) |
| Regular polygon | A = (n × a² / 4) × cot(π/n) |
How to Use the Area Calculator (Quick Steps)
- Select your shape from the dropdown (Square, Rectangle, Triangle, etc.) – a clear diagram is ready for each one.
- Fill in the required dimensions (side, base, height, diagonals, semi-axes, or angles) on the shape’s diagram. It handles decimals and common units like mm, cm, m, inches, feet – no worries!
- Select the Units dropdown to get the result in your preferred square units (like m², cm²) or miles. The tool will automatically check for consistency.
- Just press the Calculate button – you’ll instantly see the area, unit conversions, and a copy-ready result on the screen. One click!
Pro Tip: Know all three sides of a triangle? Select the Heron’s formula option – instant magic! Toggle degrees/radians for circle sectors; this tool auto-converts.
Shape-by-Shape (Formula, Worked Example, etc)
I show each formula, then a short numeric example (digit-by-digit) so you (and Google) can follow the math exactly.
Square:
Formula:
A = a2
Example:
side a = 4 m.
Square the side: 4 × 4 = 16.
Area: A = 16 m².
How to enter:
Select Square, type 4 and m and Calculate.
Use case:
Tiling a small bathroom floor.
Rectangle:
Formula:
A = l × w
Example:
length l = 3.5 m, width w = 2.1 m.
Multiply length × width: 3.5 × 2.1 = 7.35.
Area: A = 7.35 m².
How to enter:
Select Rectangle, enter 3.5 and 2.1.
Use case:
Estimating paint for a wall or flooring.
Triangle:
Formula:
A = (b × h) / 2 (when base & height known)
Heron’s formula if you know sides: A = ¼√{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}
Example (right triangle):
base b = 3 m, height h = 4 m.
Multiply base × height: 3 × 4 = 12.
Divide by 2: 12 ÷ 2 = 6.
Area: A = 6 m².
Example (Heron, sides 3, 4, 5):
Semi-perimeter s = (3 + 4 + 5) / 2 = 6.
Compute product: (s)(s−a)(s−b)(s−c) = 6 × 3 × 2 × 1 = 36.
Square root: √36 = 6.
Area: A = 6 m².
How to enter:
Triangle option lets you choose base & height or three sides (Heron).
Use case:
Land parcel triangulation; roofing triangles.
Circle:
Formula:
A = πr2
Example:
radius r = 0.5 m.
Square radius: 0.5 × 0.5 = 0.25.
Multiply by π: 0.25 × π ≈ 0.785398 m².
How to enter:
Enter radius or diameter (the tool accepts both).
Use case:
Circular garden beds, pizza area for ingredient estimates.
Semicircle:
Formula:
A = (1/2)πr2
Example:
radius r = 0.5 m.
πr2 = 0.785398 (from circle example).
Half of that: 0.785398 ÷ 2 = 0.392699 m².
How to enter:
Choose Semicircle, enter radius and units.
Use case:
Half-round windows, semicircular patios.
Ellipse:
Formula:
A = πab (a and b are semi-major and semi-minor axes)
Example:
a = 2 m, b = 1 m.
Multiply semi-axes: 2 × 1 = 2.
Multiply by π: 2 × π ≈ 6.283185 m².
How to enter:
Enter semi-major a and semi-minor b. (If you measured full axes, divide by 2 first.)
Use case:
Elliptical gardens, tracks.
Trapezoid:
Formula:
A = (a + b) × h / 2 (a and b are parallel sides)
Example:
a = 3 m, b = 5 m, h = 2 m.
Sum parallel sides: 3 + 5 = 8.
Multiply by height: 8 × 2 = 16.
Divide by 2: 16 ÷ 2 = 8 m².
How to enter:
Select Trapezoid, enter a, b, and h.
Use case:
Sloped roof sections, trapezoidal beds.
Parallelogram:
Formula:
A = base × height (or A = ab × sin(θ))
Example:
base = 4 m, height = 2 m.
Multiply: 4 × 2 = 8 m².
How to enter:
Provide base and perpendicular height; if given sides + angle, use the sin formula.
Use case:
Floor joist planning, fabric cuts.
Rhombus & Kite:
Formula (both):
A = (d1 × d2) / 2 (diagonals must be perpendicular)
Example:
d1 = 4 m, d2 = 3 m.
Multiply diagonals: 4 × 3 = 12.
Divide by 2: 12 ÷ 2 = 6 m².
How to enter:
Enter the two diagonals.
Use case:
Decorative panel areas, kite design.
Circle Sector:
Formula:
A = (r2 × θ) / 2 where θ is in radians. (If angle is in degrees, convert: θ_rad = θ_deg × π/180.)
Example:
r = 2 m, angle = 60°.
Convert angle to radians: 60° × π/180 = π/3 ≈ 1.0471976.
r2 = 4.
Multiply 4 × θ_rad = 4 × 1.0471976 = 4.1887904.
Divide by 2: 4.1887904 ÷ 2 = 2.094395 m².
How to enter:
Choose sector, enter radius and angle (degrees toggle available).
Use case:
Pizza slices, circular sector flower beds.
Regular Polygon:
Formula:
A = (n × a² / 4) × cot(π/n) where n is number of sides and a is side length.
Example (regular hexagon):
n = 6, a = 1 m.
π/6 ≈ 0.5235988.
cot(π/6) ≈ 1.7320508.
n × a² = 6 × 1 = 6.
6 ÷ 4 = 1.5.
1.5 × 1.7320508 = 2.598076 m².
How to enter:
Select Regular Polygon, enter n and a.
Use case:
Tiled pavements, gazebo roof panels.
Units and Measurement Tips (A Must-Read to Avoid Mistakes)
- Keep Units Consistent: Convert all inputs to a single unit (e.g., all meters). Complete calculations using mixed units are inverted—my number one rule in every project!
- Diameters and Semi-Axes: Measure the full axis of an ellipse or circle? Divide by 2 to find the radius/semi-axis. This is basic, but 90% of users forget it.
- Triangle Height Trick: Height unclear? Drop the perpendicular or divide the triangle into right triangles and measure. This is my go-to hack for real estate plots!
- Sector Angles Easy: Measure degrees? Turn on the calculator’s degree-to-radian toggle – sorted in one click.
- Field Methods for Irregular Shapes: Divide irregular shapes into small triangles, calculate the area of each, and add them up. Planimeters or smartphone apps are also great for irregular plots – I used them in surveys!
- Rounding Smartly: Hold on to 4-6 significant digits in intermediate steps, and only round the final result. Early rounding reduces accuracy, trust me!
Quick Copy-Paste Reference
- A = a² (Square)
- A = l × w (Rectangle)
- A = (b × h) / 2 (Triangle)
- A = πr² (Circle)
- A = (1/2)πr² (Semicircle)
- A = πab (Ellipse)
- A = (a + b) × h / 2 (Trapezoid)
- A = (d1 × d2) / 2 (Rhombus/Kite)
- A = r² × θ / 2 (Sector, θ in radians)
- A = (n × a²) / 4 × cot(π/n) (Regular polygon)
Want a printable formula card? Use the Sheet on the calculator page.
Frequently Asked Questions
A = πr² – Square the radius and multiply it by π to get the result in square units. The simplest and most powerful formula!
Use Heron’s formula: A = 1/4 √((a+b+c)(-a+b+c)(a-b+c)(a+b-c)). This is where the semi-perimeter works – a game-changer in field surveys!
A = (r² × θ) / 2 (θ in radians). To convert from degrees, θ_rad = θ_deg × π / 180 – the calculator handles it itself.
A = πab, where a and b are the semi-major and semi-minor axes. Perfect for oval shapes, they are very useful in engineering.
No, not uniquely – just like the perimeter can be the same for different shapes, the areas can be different. Shape-specific dimensions are essential; this is a rule of basic math.
Math 100% accurate; accuracy depends on your measurements and units. Measure precisely, avoid early rounding – my pro tip!
Conclusion:
Area Calculator is designed for clarity and accuracy: clearly labeled input fields, unit handling, quick examples for each shape, and sheets. Whether you’re a student, DIYer, architect, or landscaper, our tool reduces errors and saves time.